This is the complete physics on golf. It should answer all your golfing questions. After reading and deciphering all this information, what else is there?
The Physics of Golf
In order to calculate and produce a realistic ball fight
trajectory in the simulator, I had to do quite a bit of research into the
physics of golf. Here are some of the aspects that I have taken into account
that might be of interest to you.
Dimples on the ball and the Magnus effect
As you probably already know, the dimples on the golf ball are
there to give the ball more lift and reduced drag during its flight and therefore increase its
carry through the air.

This graph - which was generated by
the GGS trajectory
calculation routines - shows just what a difference those little dimples
actually make to the distance the ball will travel. As you can see, a
ball with
the appropriate depth dimples and top spin will travel far further than a
ball
with no dimples at all. Those little dimples actually scope the air on
its front
and top surface and throw it back behind the ball. This causes
turbulence which
prevents the pressure behind the ball from falling and thus the pull
back effect
that would have. It also causes the air-flow above the ball to travel
faster and
thus the pressure on the ball from the top to be lower than the air
pressure below the ball. This pressure difference (i.e. more relative
pressure from below
than on top) causes the ball to lift and stay in the air for a longer
time. This
phenomenon is known as the Magnus effect


Drag behind a spinning golf ball with and without dimples
Ball Spin
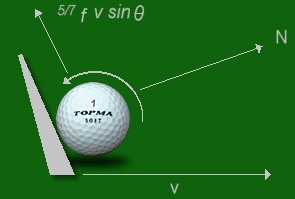
This pushing and lifting effect is
dependent on the top-spin rate of the ball. When the ball is struck
properly by a lofted club, the ball will tend to travel or roll up the
club-face before it is launched. This causes the ball to anti-clockwise
spin at a rate governed by the speed, loft and surface friction of the
club head face at impact. Typical ball spin-rates are:
3,600 rpm when hit with a 10° driver (8° launch angle) at a
velocity of 134 mph
7,200 rpm when hit with a 5 iron (23° launch angle) at a
velocity of 105 mph
10,800 rpm when hit with a 9 iron (45° launch angle) at a
velocity of 90 mph
Topping the ball (i.e.. when the
bottom of the club-face hits the ball above its center) will cause the
ball to spin in the other direction - i.e.. downward - which will cause
the ball to dive into the ground.

With really high spin rates the magnus lifting effect will
actually increase the ball's rate of climb. The effect is known as blow-up and
usually remains the domain of the real hard hitters.

Of course the wind strength and direction will also affect the ball's flight.
Apart from this top and bottom spin around the ball's
horizontal axis, there is also the amount of side spin that the ball may
have. The side spin is induced by the club hitting the ball with an open or
closed face at a path other than 90° to the ball's intended
direction.
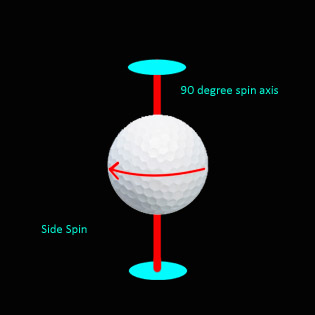
The Slice
Hitting the ball with an open club-face and a club-path from
out to in will cause the ball to spin from left to right. The ball's flight will
then curve to the right or 'Slice'.
The Hook
Hitting the ball with a closed club-face and a club-path from
in to out will cause the ball to spin from right to left. The ball's
flight will then curve to the left or 'Hook'.
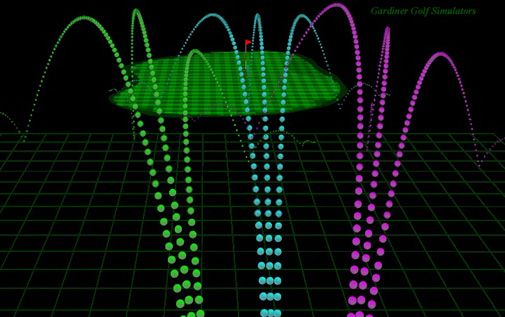
Golf ball flight trajectory traces in the GGS system.
From left to right: Pull-hook, pull, pull-slice, straight-hook ,
straight, straight-slice, push-hook, push and push-slice.
Average Distances
-
3-IRON : 170-190 yds
(155-174m)
-
4-IRON : 160-180 yds
(146-163m)
-
5-IRON : 150-170 yds
(137-155m)
-
6-IRON : 140-160 yds
(128-146m)
-
7-IRON : 130-150 yds
(119-137m)
-
8-IRON : 120-140 yds
(110-128m)
-
9-IRON : 110-130 yds
(101-119m)
-
Pitching : 90-110 yds (82-101m)
-
Sand Wedge: up to 80 yds (73m)
-
DRIVER : 200-240 yds
(183-219m)
-
3-WOOD : 190-220 yds
(174-201m)
-
5-WOOD : 170-190 yds
(155-174m)
-
7-WOOD : 160-180 yds
(146-165m)
Calculating Flight Trajectories
Now's the time to put all this physical theory into
practice.
Basic parabolic flight
If a golf ball didn't have any dimples and we neglect any
other aerodynamic effects such as drag and wind, then the trajectory calculation
is really very simple.
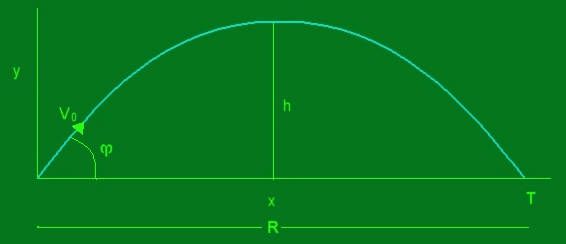
For any given time (t) the distance traveled (x component)
is
x(t) = (Vo cosm)t
and the height (y component) at any given time (t) is
y(t) = (Vo sinm)) - (gt²)/2
where Vo = initial velocity of ball
g = gravitational acceleration 9.8 m/s/s
m = the launch angle in
radians
All simple stuff but unfortunately - for me that is - a golf
ball's trajectory is not that simple and thus not that simple to calculate.
First off we've got that Magnus effect (lift on a spinning
dimpled ball) to apply. In my system I have used the following formula to
estimate the Magnus lift force :
FL = (dvr4
av 2di²)(2r)
where d = density of air at 60° = 2.37 * 10-³
v = velocity
r = ball radius
av = angular velocity in radians per second (if you have
spin, n, in rpm, them av = (2pi n)/60
An adapted version of the same formula is also used to determine the force on the x
plane (left/right direction) which causes the ball to curve. The vertical and
horizontal spin rates of the ball are calculated from the incoming data feed
from the sensor mat in the system.
Then we have the wind force and air drag to deal with which acts on all of
the 3 dimensions of the flight (x,y,z) whereby
x is the left/right direction/deviation of the ball flight
y is the height
and z the distance traveled ahead
The drag force can be written as:
Fd = -Cdv
Fd = -Cdvx
-Cdvy
-Cdvz
where Cd is
the drag coefficient, v is the velocity of the ball (vx,vy,vz
are its components) and the minus sign means that this drag force opposes the
ball's motion.
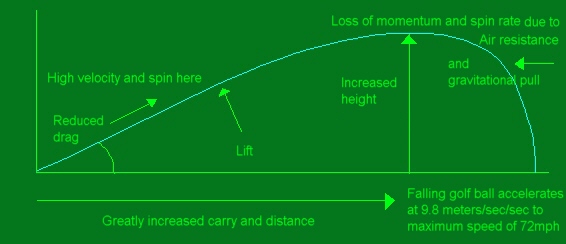
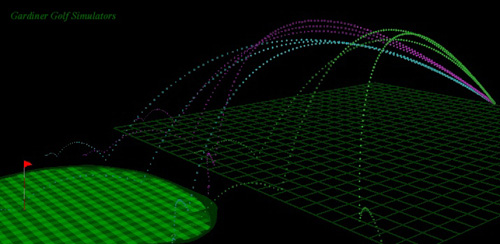
The side view of the trajectory will then look something like this.
Terminal velocity
Due to air resistance a falling
golf ball will not continue on accelerating at the rate of 9.8 meters /
per second / per second. It will eventually reach a maximum falling
velocity dictated by its mass and area. This velocity is known as
Terminal Velocity and in the case of a golf ball with a radius of 2.1
cm, an area of 14cm² and a mass of 46 grams, this will be 32
meters per second or 72 mph.
Wind force
Wind force is defined as
Fw = -Cwvw
where Cw is the drag coefficient
and vw is the wind speed.
Defining the wind direction as measured by angle y
I use the following formulas to determine the x and z components
of the wind force on the ball:
Fxw = Fw
cos y = -cos y(Cwvw)
Fzw = Fw
cos y = -sin y
(Cwvw)

If there is any side spin on the ball - and there usually is -
then the ball will curve in the direction of the spin.
Side wind will, of course, cause the ball to curve in its direction and head or tail wind will affect the ball's carry.
Also of interest is the research work done by P.W. Bearman and J.K. Harvey
(P.W. Bearman and J.K. Harvey - Golf ball aerodynamics, Aeronautical Quarterly, pp. 112 - 122, May
1976 ) The following formulas are used to calculate the height, distance,
acceleration and velocity of a flying golf ball for any given time t - n=0
to n= (until ball hits ground)
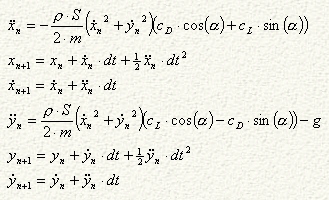
Where:
-
p is density of air at sea level = 1.225 kg/m3
-
S is on stream surface ( = pi r², r = 20.55 mm) = 1.3267×10-³
m²
-
'm' is mass of the ball = 0.050 kg
-
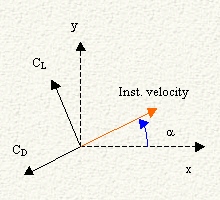
a is the instantaneous angle between the instantaneous velocity and the horizon.
-
CD is the drag coefficient, which has the same direction as the instantaneous velocity.
-
CL is the lift coefficient, which direction is perpendicular to the instantaneous velocity.
-
dt is the time step ('step size'). After every time step the simulation will be recalculated.
-
'x' is the coordinate in the direction of the range.
-
'y' is the coordinate in the direction of the height.
Collision theory

When the clubface collides with the ball it's total contact
time is approximately 0.0005 seconds and the peak force applied to the ball can be as high as 4000
pounds
.
This high force actually compresses the ball at impact.
Due to the elasticity of the ball (compression) and the clubface (Metal
woods) the ball
will be launched at a higher velocity than that of the club head at impact.
Average factors are 1.46 for a driver, 1.30 for a 5 iron and 1.12 for a 9
iron.
i.e. the ball's speed just after impact will be this factor
greater than the club head speed
Calculating ball launch velocities
Formulas used to determine this increase in ball velocity are:
vball = ((velc*(1.67))/(1.0+(ball/mass)))
where :
vball = the velocity of the ball
velc = club head speed.
ball = mass of ball
mass = mass of club head
and 1.67 = coefficient of restitution
The coefficient of restitution (1.67)
accounts for momentum loss and the fraction of the energy into a collision that a collision "gives back."
Including the loft of the club the formula is:
vballi = ((cos (loft))^2*(sin(90-loft))*vball
where:
Vballi = Velocity of the ball after impact with a
lofted club
vball = ((velc*(1.67))/(1.0+(ball/mass)))
loft = Loft of the club
90-loft = The compliment of the loft of the club
vball = The velocity of the ball determined by the previous formula.
Calculating Spin Rates

The equation 5/7 f v
sin 0 is used to calculate the vertical velocity of the ball traveling
up the club head face where f is the fraction of speed remaining when the
compression of the ball is considered, 0 is the angle of the
clubface at impact and v is the velocity of the club head.

To calculate the side spin I use an adapted version of the
same formula using the degrees the clubface is open or closed in relation to the
club head path.
Knowing the ball velocity and the circumference of the golf
ball the theoretical spin rate can be calculated as:
spin rate in rpm = (bv / c) /60
where c = circumference of the golf ball = 0.043m and
bv = 5/7 f v
sin 0
Both top spin and side spin are used to produce a ratio of the
true spin rpm and direction
i.e. if top spin = 3600 rpm at 0° and side spin = 900 rpm at
90° or -90° (left or right) then
ratio = 900:3600 = 0.25
assuming a ratio of 1:1 would result in a spin direction (or
axis tilt) of 45°
then spin direction = 45° * 0.25 = 11.25°
Bounce

When the golf ball eventually hits the ground, it will tend to
bounce a number of times whereby the height and angle of the bounce is very
dependent upon what type of surface it hits.
When the golf ball hits a hard
surface like a footpath, then the bounce will be very profound (aprox.
50% of its falling height). However, most of the time it will hit the
fairway or the green - hopefully - or maybe in the rough. Here the
energy absorbed by this type of surface is very significant and the ball
will only bounce a fraction of what it would if it had hit a hard
smooth surface.
In my system I have created formulas that take all these
factors into account including the deviation the angle of bounce will have on
inclined soft surface. This is not the same as on a hard surface like a
footpath or hitting a tree trunk. On a hard surface we can say that the angle
the bounce flight will be near the angle of impact reversed. However, on a soft(er)
surface, because of the energy absorbed, the angle of bounce launch will be more
towards the surface angle normal.
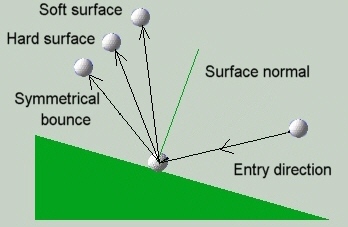
Rolling on inclined planes
After the ball has stopped bouncing
and landed it will tend to roll for a certain distance. If the plane is
horizontal then the amount of roll can be calculated from its velocity
and the friction of the surface.
If, however, the ball lands on an inclined plane, then we have
to take into account the force the angle of the plane will have on the ball.
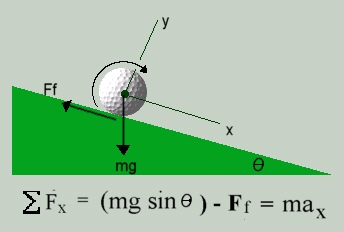
The above formula is used to calculate the force on the ball
in the x direction up and down a plane, where mg is the force due
to gravity, Ff the opposing force due to friction and ax
is the linear acceleration in the x direction. The friction force is
equal to us N where
us is the coefficient
of friction of the surface and N is the normal
reaction force between the ball and the plane.
Things start to get a bit
complicated - to say the least - when the ball is rolling on a contoured
surface like a green. Here I have to make continual calculations and
adjustments to the direction and speed of the ball taking into account
the momentum the ball has in a certain direction. At each time step I
check the slope angle and direction and calculate a curve for the ball
to follow depending on the magnitude of the force the slope is exerting
on the ball. If, at any following steps this slope changes, I
recalculate the curve and apply this to its current path at a rate
governed by its current velocity or momentum.

When all the calculations of the flight trajectory, bounce and
roll are done, the results are stored in a table. This table contains the 3
dimension (z,x and y) co-ordinates of all the steps and is in turn read by the
flight routines. When the system gets the launch (fire) command from the sensor
mat and all the club head and clubface angle and velocity data have been read,
the system calculates the trajectory and a timer is started to produce timer
events at 0.05 second intervals. The timer event handler then reads the next
coordinates for the step from the flight trajectory table, removes the image of
the ball on the screen at the last step and displays it again at the new
position. The 'Trajectory Trail On" feature of the system prevents the
system from removing the ball image so the user can see the exact trail of the
trajectory. This feature had been switched on for all the screen shots shown on
this site.
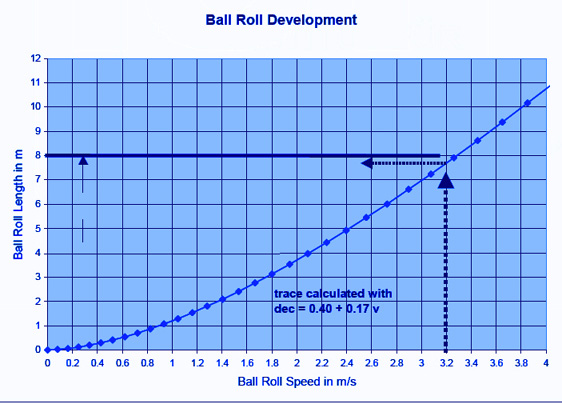
The above graph shows the distance a ball will roll for a
given initial velocity and a given green speed.
The GGS system allows you to vary the graph used in the ball
roll calculations from linear to exponential as well as the green
speed.
Ball Velocity/Carry Graph for all clubs
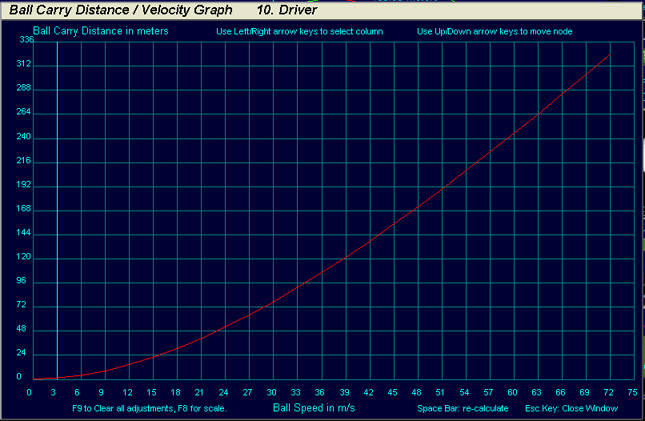
You can see and adjust the ball carry for every club and for
every ball velocity.

"C makes it easy to shoot yourself in the foot; C++
makes it harder, but when you do it blows your whole leg off."